A Triangle With a 45 Degrees Angle in Square : A very hard problem from Geometry

Let P and Q be the points where AN and AM intersect the diagonal BD, respectively. It is noted that ∠QAN=∠QDN=45∘.Thus, AQND is a cyclic quadrilateral, therefore implying that ∠AQN=90∘.

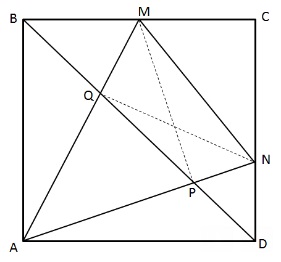
This in turn implies that ΔAQN is a right-isoceles triangle with AN as the hypotenuse. Thus, AQ=AN2–√.

The same argument can be employed to show that AP=AM2–√.

Now, since triangles APQ and AMN share a common vertex angle A, we have, Area(ΔAPQ)Area(ΔAMN)=AQ⋅APAM⋅AN. However, from the conclusions in the previous two paragraphs, we have AQAN=APAM=12–√.

This therefore implies that Area(ΔAPQ)Area(ΔAMN)=12, or equivalently, Area(ΔAPQ)Area(MNPQ)=1, as claimed by the problem.

The problem, due to V. Proizvolov, appeared in Kvant - a popular Russian magazine - (#1, 2004, M1895), with a solution in a later issue (#4, 2004).

Class IX West Bengal Board Ganit Prakash Chapter 20 Solutions- Co-ordinate Geometry

Class IX West Bengal Board Ganit Prakash Chapter 20 Solutions - Coordinate Geometry

In this pdf you will get all the solved problem from the exercise 20. Before going through the solutions you are advised to first try the problem yourself. If you get stuck, seek help from the solutions. Don't copy blindly. If you have any query, comment below.