Functions
A relation ‘f’ is said to be a function, if every element of a non-empty set X, has only one image or range to a non-empty set Y.
Or
If ‘f’ is the function from X to Y and (x,y) ∊ f, then f(x) = y, where y is the image of x, under function f and x is the preimage of y, under ‘f’. It is denoted as;
f: X → Y.
Example: N be the set of Natural numbers and the relation R be defined as;
R = {(a,b) : b=a2, a,b ∈ N}. State whether R is a relation function or not.
Solution: From the relation R = {(a,b) : b=a2, a,b ∈ N}, we can see for every value of natural number, their is only one image. For example, if a=1 then b =1, if a=2 then b=4 and so on.
Therefore, R is a relation function here.
Real-Valued Function
A function f : A → B is called a real-valued function if B is a subset of R (set of all real numbers). If A and B both are subsets of R, then f is called a real function.
Some Specific Types of Functions
Identity function: The function f : R → R defined by f(x) = x for each x ∈ R is called identity function.
Domain of f = R; Range of f = R
Constant function: The function f : R → R defined by f(x) = C, x ∈ R, where C is a constant ∈ R, is called a constant function.
Domain of f = R; Range of f = C
Polynomial function: A real valued function f : R → R defined by f(x) = a0 + a1x + a2x2+…+ anxn, where n ∈ N and a0, a1, a2,…….. an ∈ R for each x ∈ R, is called polynomial function.
Signum function: The real function f : R → R defined
by f(x) =
or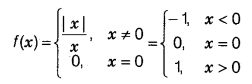
is called the signum function.
Domain of f = R; Range of f = {-1, 0, 1}
Greatest integer function: The real function f : R → R defined by f (x) = {x}, x ∈ R assumes that the values of the greatest integer less than or equal to x, is called the greatest integer function.
Domain of f = R; Range of f = Integer
Fractional part function: The real function f : R → R defined by f(x) = {x}, x ∈ R is called the fractional part function.
f(x) = {x} = x – [x] for all x ∈R
Domain of f = R; Range of f = [0, 1)
Algebra of Real Functions
Addition of two real functions: Let f : X → R and g : X → R be any two real functions, where X ∈ R. Then, we define (f + g) : X → R by
{f + g) (x) = f(x) + g(x), for all x ∈ X.
Subtraction of a real function from another: Let f : X → R and g : X → R be any two real functions, where X ⊆ R. Then, we define (f – g) : X → R by (f – g) (x) = f (x) – g(x), for all x ∈ X.
Multiplication by a scalar: Let f : X → R be a real function and K be any scalar belonging to R. Then, the product of Kf is function from X to R defined by (Kf)(x) = Kf(x) for all x ∈ X.
Multiplication of two real functions: Let f : X → R and g : X → R be any two real functions, where X ⊆ R. Then, product of these two functions i.e. f.g : X → R is defined by (fg) x = f(x) . g(x) ∀ x ∈ X.
Quotient of two real functions: Let f and g be two real functions defined from X → R. The quotient of f by g denoted by 




