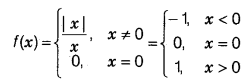Combinations - RD Sharma Solved Problems

 

What is a Combination?

A combination is a mathematical technique that determines the number of possible arrangements in a collection of items where the order of the selection does not matter. In combinations, you can select the items in any order.

Combinations can be confused with permutations. However, in permutations, the order of the selected items is essential. For example, the arrangements ab and ba are equal in combinations (considered as one arrangement), while in permutations, the arrangements are different.

Formula for Combination

Mathematically, the formula for determining the number of possible arrangements by selecting only a few objects from a set with no repetition is expressed in the following way:

 

 

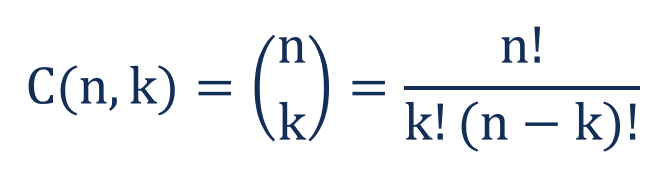
Where:

• n – the total number of elements in a set
• k – the number of selected objects (the order of the objects is not important)
• ! – factorial

A few important results on combinations are as follows:

• The number of ways of selecting n objects out of n objects is:${}^n{C}_n=\frac{n!}{n!\left(n-n\right)!}=\frac{n!}{n!0!}=1$
• The number of ways of selecting 0 objects out of n objects is:${}^n{C}_0=\frac{n!}{0!\left(n-0\right)!}=\frac{n!}{0!n!}=1$
• The number of ways of selecting 1 object out of n objects is: ${}^n{C}_1=\frac{n!}{1!\left(n-1\right)!}=\frac{n\times \left(n-1\right)!}{\left(n-1\right)!}=n$
• ${}^n{C}_r{=}^n{C}_{n-r}$
• ${}^n{C}_r{+}^n{C}_{r-1}{=}^{n+1}{C}_r$

Indian Statistical Institute : Solved Problems

TOMATO (TEST OF MATHEMATICS AT THE 10+2 LEVELS) 

OBJECTIVE PROBLEM SOLVING

 

ISI's Test of Mathematics at 10 + 2 Level is a rigorous book for mathematics enthusiasts and for Class-12 students applying for an admission into the Bachelor of Mathematics at one of the Indian Statistical Institutes across the nation. The book provides advanced problems that are commonly found in the ISI entrance examinations and also prepares students for a study involving higher mathematics.

About the Indian Statistical Institute

ISI is an academic institute in India catering to studies in statistics. It was established in 1931 to improve the application of statistical methods across the nation. The institute provides academic programs at the undergraduate and postgraduate level in mathematics, statistics and numerical methods.

PART -1 QUESTION 1 TO QUESTION 28

Permutations - RD Sharma Solved Problems.

 A permutation is an arrangement of objects in a definite order. The members or elements of sets are arranged here in a sequence or linear order. For example, the permutation of set A={1,6} is 2, such as {1,6}, {6,1}. As you can see, there are no other ways to arrange the elements of set A.

In permutation, the elements should be arranged in a particular order whereas in combination the order of elements does not matter. Also, read: Permutation And Combination

When we look at the schedules of trains, buses and the flights we really wonder how they are scheduled according to the public’s convenience. Of course, the permutation is very much helpful to prepare the schedules on departure and arrival of these. Also, when we come across licence plates of vehicles which consists of few alphabets and digits. We can easily prepare these codes using permutations.

A permutation is defined as an arrangement in a definite order of a number of objects taken, some or all at a time. Counting permutations are merely counting the number of ways in which some or all objects at a time are rearranged. The convenient expression to denote permutation is defined as “ nPr ”.

The permutation formula is given by,

Pr = n!/(n-r)! ; 0 ≤ r ≤ n

Where the symbol “!” denotes the factorial which means that the product of all the integers is less than or equal to n but it should be greater than or equal to 1.

Permutation When all the Objects are Distinct

There are some theorems involved in finding the permutations when all the objects are distinct. They are :

Theorem 1: If the number of permutations of n different objects taken r at a time, it will satisfy the condition 0 < r ≤ n and the objects which do not repeat is n ( n – 1) ( n – 2)……( n – r + 1), then the notation to denote the permutation is given by “ n Pr”

Theorem 2: The number of permutations of different objects “n” taken r at a time, where repetition is allowed and is given by nr .

Permutation When all the Objects are not Distinct Objects

Theorem 3: To find the number of permutations of the objects ‘n’, and ‘p’s are of the objects of the same kind and rest is all different is given as n! / p!

Theorem 4: The number of permutations of n objects, where p1 are the objects of one kind, p2 are of the second kind, …, pk is of the kth kind and the rest, if any, are of a different kind, then the permutation is given by n! / ( p1!p2!…Pk!)

Functions Class XI - RD Sharma Solved Problems

 Functions

A relation ‘f’ is said to be a function, if every element of a non-empty set X, has only one image or range to a non-empty set Y.

Or

If ‘f’ is the function from X to Y and (x,y) ∊ f, then f(x) = y, where y is the image of x, under function f and x is the preimage of y, under ‘f’. It is denoted as;

f: X → Y.

Example: N be the set of Natural numbers and the relation R be defined as;

R = {(a,b) : b=a2, a,b ∈ N}. State whether R is a relation function or not.

Solution: From the relation R = {(a,b) : b=a2, a,b ∈ N}, we can see for every value of natural number, their is only one image. For example, if a=1 then b =1, if a=2 then b=4 and so on.

Therefore, R is a relation function here.

Real-Valued Function
A function f : A → B is called a real-valued function if B is a subset of R (set of all real numbers). If A and B both are subsets of R, then f is called a real function.

Some Specific Types of Functions
Identity function: The function f : R → R defined by f(x) = x for each x ∈ R is called identity function.
Domain of f = R; Range of f = R

Constant function: The function f : R → R defined by f(x) = C, x ∈ R, where C is a constant ∈ R, is called a constant function.
Domain of f = R; Range of f = C

Polynomial function: A real valued function f : R → R defined by f(x) = a0 + a1x + a2x2+…+ anxn, where n ∈ N and a0, a1, a2,…….. an ∈ R for each x ∈ R, is called polynomial function.

Signum function: The real function f : R → R defined
by f(x) = |x|x, x ≠ 0 and 0, if x = 0
or

is called the signum function.
Domain of f = R; Range of f = {-1, 0, 1}

Greatest integer function: The real function f : R → R defined by f (x) = {x}, x ∈ R assumes that the values of the greatest integer less than or equal to x, is called the greatest integer function.
Domain of f = R; Range of f = Integer

Fractional part function: The real function f : R → R defined by f(x) = {x}, x ∈ R is called the fractional part function.
f(x) = {x} = x – [x] for all x ∈R
Domain of f = R; Range of f = [0, 1)

Algebra of Real Functions
Addition of two real functions: Let f : X → R and g : X → R be any two real functions, where X ∈ R. Then, we define (f + g) : X → R by
{f + g) (x) = f(x) + g(x), for all x ∈ X.

Subtraction of a real function from another: Let f : X → R and g : X → R be any two real functions, where X ⊆ R. Then, we define (f – g) : X → R by (f – g) (x) = f (x) – g(x), for all x ∈ X.

Multiplication by a scalar: Let f : X → R be a real function and K be any scalar belonging to R. Then, the product of Kf is function from X to R defined by (Kf)(x) = Kf(x) for all x ∈ X.

Multiplication of two real functions: Let f : X → R and g : X → R be any two real functions, where X ⊆ R. Then, product of these two functions i.e. f.g : X → R is defined by (fg) x = f(x) . g(x) ∀ x ∈ X.

Quotient of two real functions: Let f and g be two real functions defined from X → R. The quotient of f by g denoted by fg is a function defined from X → R as

Relations Class XI - RD Sharma Solved Problems

Cartesian Product of Sets

Suppose there are two non-empty sets A and B. So, the cartesian product of A and B is the set of all ordered pairs of elements from A and B.

A × B = {(a,b) : a ∊ A, b ∊ B}

Let A = {a1, a2, a3, a4} and B = {b1, b2}

Then, The cartesian product of A and B will be;

A × B = {(a1, b1), (a2, b1), (a3, b1), (a4, b1), (a1, b2), (a2, b2), (a3, b2), (a4, b2)}

Example: Let us say, X = {a,b,c} and Y = { 1,2,3}

Therefore, X × Y = {(a, 1), (a, 2), (a, 3), (b, 1), (b, 2), (b, 3), (c, 1), (c, 2), (c, 3)}.

This set has 9 ordered pairs. We can also represent it as in a tabular form.

Note: Two ordered pair X and Y are equal, if and only if the corresponding first elements and second elements are equal.

Relations

Definition: A relation R is the subset of the cartesian product of X x Y, where X and Y are two non-empty elements. It is derived by stating the relationship between the first element and second element of the ordered pair of X × Y. The set of all primary elements of the ordered pairs is called a domain of R and the set of all second elements of the ordered pairs is called a range of R.

For two sets X = {a, b, c} and Y = {apple, ball, cat}, the cartesian product have 9 ordered pairs, which can be written as;

X × Y = {(a, apple), (a, ball), (a, cat), (b, apple), (b, ball), (b, cat), (c, apple), (c, ball), (c, cat)}

With this we can obtain a subset of X x Y by introducing a relation R, between the elements of X and Y as;

R = {(a,b) : a is the first letter of word b, a ∊ X, b ∊ Y}

Therefore, the relation between X and Y can be represented as;

R = {(a,apple),(b,ball),(c,cat)}

Example: Let X={a,b} and Y = {c,d}. Find the number of relations from X to Y.

Solution: X × Y = {(a,c),(a,d),(b,c),(b,d)}

Number of subsets, n (X × Y) = 24 . Therefore, the number of relations from X to Y is 24.

Solved Problems from the book of RD Sharma - Class XI CBSE

Mathematics Project Class XI - West Bengal Board

 Preparation of Project Work- Mathematics -XI Science

Final Date of Submission 30th January 2023( No other submission date will be provided)

Each student has to select one topic from Group-A and one topic from Group-B. Two separate files (to be collected from school) must be made. (one for each group)

The cover page must clearly contain the following information:

NAME OF SCHOOL

STUDENT'S NAME, 

CLASS-XI, SECTION & ROLL NUMBER

SUBJECT

TOPIC 

GROUP A or B

REGISTRATION NUMBER

The same information must also be registered on the first page of your copy.

Topic Group-A ( Choose any one of the following)

                 Topic Group-B ( Choose any one of the following)

IMPORTANT INSTRUCTIONS:

        I. Don't print and paste images, tables or graphs from the internet. If any graph or sketch is needed, you must prepare it on your own using graph paper & pencil.

        II. Give proper examples and diagrams as needed.

        III. USE SEPARATE COPIES FOR DIFFERENT GROUP.

        IV. USE COPIES PROVIDED BY THE SCHOOL. 

        V.  Write on one side of the paper.

Project Writing: 

Use the following structure to complete your project:

Cover Page: All details as described earlier.

First Page: Same details as on cover page.

Then divide your work in the following sections:

            1. INTRODUCTION

            2. DESCRIPTION

            3. CONCLUSION

           4. BIBLIOGRAPHY

Give appropriate graphs/diagrams and examples whenever necessary. 

Marks Distribution: (20 Marks)

        Presentation: 4 (Group-A) + 4 (Group-B)

        Note Book: 4 (Group-A) + 4 (Group-B)

        Viva-Voce: 4

        

CBSE CLASS XII Mathematics Term I Board Paper 2021 Solved