Problem for #jeemains #WBJEE #CBSE #ISC #mathematics
In a company, 15% of the employees are graduates and 85% of the employees are non-graduates. as per the annual report of the company, 80% of the graduate employees and 10% of the non-graduate employees are in the administrative positions. find the probability that an employee selected at random from those working in administrative positions will be a graduate.
Answer:
Step-by-step explanation:
Let G be the event that the selected employee is a graduate, and NG be the event that the selected employee is non-graduate.
Clearly, G and NG forms a mutually exclusive and exhaustive set of events.
Further, let A be the event that the selected employee works in administrative office.
According to the problem, we have to find, the selected employee is a graduate given he/she works in the administrative position P(G/A).
By Bayes' theorem,
Now, Probability of an employee to be graduate =
Probability of an employee to be non-graduate =
Probability of an employee working in administrative office given he is a graduate =
Probability of an employee working in administrative office given he is a non-graduate =
Substituting the values in
1. An executive committee of 6 is to be formed from 4 ladies
and 7 gentlemen. In how many ways can this be formed when the committee
contains (i) only 2 lady members, (ii) at least 2 lady members?
2. Find the number of committees of 5 members that can be
formed from 6 gentlemen and 4 ladies if each committee has at least one lady
and two gentlemen.
3. A committee of 5 is to be formed from six ladies and four
gentlemen. In how many ways this can be done so that the committee contains (i)
exactly two ladies, (ii) at least two ladies, (iii) at most two ladies?
4. In a cricket team of 14 players 6 are bowlers. How many
different teams of 11 players can be selected keeping at least 4 bowlers in the
team?
5. A box contains 12 lamps of which 5 are defective. In how
many ways can a sample of 6 be selected at random from the box so as to include
at most 3 defective lamps?
6. An examinee is required to answer 6 questions out of 12
questions which are divided into two groups each containing 6 questions, and he
is not permitted to answer more than 4 questions from any group. In how many
ways can he answer 6 questions?
7. A question paper contains 10 questions, which are divided
into two groups each containing 5 questions. A candidate is asked to answer 6
questions only, and to choose at least 2 questions from each group. In how many
different ways can the candidate make up his choice?
8. In how many ways can a team of 11 cricketers be chosen
from 9 batsmen and 6 bowlers to give a majority of batsman if at least 3 bowlers
are to be included?
9. The Indian Cricket Eleven is to be selected out of
fifteen players, five of them are bowlers. In how many ways the team can be
selected so that the team contains at least three bowlers?
10. How many combinations can be formed of eight counters
marked 1, 2, 3, 4, 5, 6, 7, 8 taking them 4 at a time, there being at least one
odd and one even counter in each combination?
11. Find the number of permutations of the letters of the
words FORECAST and MILKY taking 5 at a time of which 3 letters from the first
word and 2 from the second.
12. In how many ways can the crew of an eight-oared boat be
arranged if 2 of the crew can row only on the stroke side and 1 can row only on
the bow side?
13. Of the 17 articles, 12 are alike and the remaining 5 are
different. Find the number of combinations, if 13 articles are taken at a time.
14. Out of 3n given things 2n are alike and the rest are
different. Show that a selection of 2n things can be made from these 3n things
in 2" different ways.
15. Show that there are 136 ways of selecting 4 letters from
the word EXAMINATION.
16. Find the total number of ways of selecting 5 letters
from the letters of the word INDEPENDENT.
17. (i) Find the number of combinations in the letters of
the word STATISTICS taken 4 at a time.
(ii) Find the
number of permutations in the letters of the word PROPORTION taken 4 at a time.
18. How many different numbers of 4 digits can be formed
with the digits 1, 1, 2, 2, 3, 4?
19. (i) From 4 apples, 5 oranges mangoes, how many
selections of fruits can be made, taking at least one of each kind if the
fruits of the same kind are of different shapes?
(ii) In how many ways can one or more fruits be selected
from 4 apples, 5 oranges and 3 mangoes, if the fruits of the same kind be of
the same shape?
20. Find the total number of combinations taking at least
one green ball and one blue ball, from 5 different green balls, 4 different
blue balls and 3 different red balls.
21. How many different algebraic quantities can be formed by
combining a, b, c, d, e with + and - signs, all the letters taken together?
22. There are n points in space, no four of which are in the
in the same place with the exception of m points, all of which are in the same
plane. How many planes can be formed by joining them?
23. n1, n2 and n3,
points are given on the sides BC, CA and AB respectively of the triangle ABC.
Find the number of triangles formed by taking these given points as vertices of
a triangle.
24. A man has 7 relatives, 4 of them are ladies and 3
gentlemen; his wife has also 7 relatives, 3 of them are ladies and 4 are
gentlemen. In how many ways can they invite dinner party of 3 ladies and 3
gentlemen so that there are 3 of the man's relatives and 3 of the wife's
relatives?
25. Eighteen guests have to be seated, half on each side of long table. Four particular guests desire to sit on one particular side and three others on the other side Determine the number of ways in which the arrangements can be made.
Solved problems from the book of SN Dey Class XI WBCHSE, Permutations [ 4 and 5 marks only]
1. Trigonometric functions of Standard Angles [ 4 and 5 marks ]
Introduction of Vectors Solved Problems SN Dey - Long Answer Type Questions 5 Marks
The concept of set serves as a fundamental part of the present day mathematics. Today this concept is being used in almost every branch of mathematics. Sets are used to define the concepts of relations and functions. The study of geometry, sequences, probability, etc. requires the knowledge of sets. The theory of sets was developed by German mathematician Georg Cantor (1845-1918). He first encountered sets while working on “problems on trigonometric series”. In this Chapter, we discuss some basic definitions and operations involving sets.
The set with no elements or null elements is called an empty set. This is also called a Null set or Void set. It is denoted by {}.
For example: Let, Set X = {x:x is the number of students studying in Class 6th and Class 7th}
Since we know a student cannot learn simultaneously on two classes, therefore set X is an empty set.
The set which has only one element is called a singleton set.
For example, Set X = { 2 } is a singleton set.
Finite sets are the one which has a finite number of elements, and infinite sets are those whose number of elements cannot be estimated, but it has some figure or number, which is very large to express in a set.
For example, Set X = {1, 2, 3, 4, 5} is a finite set, as it has a finite number of elements in it.
Set Y = {Number of Animals in India} is an infinite set, as there is an approximate number of Animals in India, but the actual value cannot be expressed, as the numbers could be very large.
Two sets X and Y are said to be equal if every element of set X is also the elements of set Y and if every element of set Y is also the elements of set X. It means set X and set Y have the same elements, and we can denote it as;
X = Y
For example, Let X = { 1, 2, 3, 4} and Y = {4, 3, 2, 1}, then X = Y
And if X = {set of even numbers} and Y = { set of natural numbers} the X ≠ Y, because natural numbers consist of all the positive integers starting from 1, 2, 3, 4, 5 to infinity, but even numbers starts with 2, 4, 6, 8, and so on.
A set X is said to be a subset of set Y if the elements of set X belongs to set Y, or you can say each element of set X is present in set Y. It is denoted with the symbol as X ⊂ Y.
We can also write the subset notation as;
X ⊂ Y if a ∊ X
a ∊ Y
Thus, from the above equation, “X is a subset of Y if a is an element of X implies that a is also an element of Y”.
Each set is a subset of its own set, and a null set or empty set is a subset of all sets.
The power set is nothing but the set of all subsets. Let us explain how.
We know the empty set is a subset of all sets and every set is a subset of itself. Taking an example of set X = {2, 3}. From the above given statements we can write,
{} is a subset of {2, 3}
{2} is a subset of {2, 3}
{3} is a subset of {2, 3}
{2, 3} is also a subset of {2, 3}
Therefore, power set of X = {2, 3},
P(X) = {{},{2},{3},{2,3}}
A universal set is a set which contains all the elements of other sets. Generally, it is represented as ‘U’.
For example; set X = {1, 2, 3}, set Y = {3, 4, 5, 6} and Z = {5, 6, 7, 8, 9}
Then, we can write universal set as, U = {1, 2, 3, 4, 5, 6, 7, 8, 9,}
Note: From the definition of the universal set, we can say, all the sets are subsets of the universal set. Therefore,
X ⊂ U
Y ⊂ U
And Z ⊂ U
A union of two sets has all their elements. It is denoted by ⋃.
For example, set X = {2, 3, 7} and set Y = { 4, 5, 8}
Then union of set X and set Y will be;
X ⋃ Y = {2, 3, 7, 4, 5, 8}
Properties of Union of Sets:
X ⋃ Y = Y ⋃ X ; Commutative law
(X ⋃ Y) ⋃ Z = X ⋃ (Y ⋃ Z)
X ⋃ {} = X ; {} is the identity of ⋃
X ⋃ X = X
U ⋃ X = U
Set of all elements, which are common to all the given sets, gives intersection of sets. It is denoted by the symbol ⋂.
For example, set X = {2, 3, 7} and set Y = {2, 4, 9}
So, X ⋂ Y = {2}
The difference of set X and set Y is such that, it has only those elements which are in the set X and not in the set Y.
i.e. X – Y = {a: a ∊ X and a ∉ Y}
In the same manner, Y – X = {a: a ∊ Y and a ∉ X}
For example, if set X = {a, b, c, d} and Y = {b, c, e, f} then,
X – Y = {a, d} and Y – X = {e, f}
If two sets X and Y have no common elements, and their intersection results in zero(0), then set X and Y are called disjoint sets.
It can be represented as; X ∩ Y = 0
The West Bengal Joint Entrance Examinations Board
The West Bengal Joint Entrance Examinations Board (WBJEEB) was established in 1962 by Government of West Bengal in exercise of the powers conferred under article 162 of the Constitution of India in pursuant to No. 828-Edn(T), dated 02.03.1962.
Subsequently in 2014, the Government of West Bengal enacted the West Bengal Act XIV of 2014 to form The West Bengal Joint Entrance Examinations Board and empowered it to conduct Common Entrance Examinations for selection of candidates for admission to undergraduate and postgraduate Professional, Vocational and General Degree Courses in the State of West Bengal and to conduct on-line counselling process or otherwise adopting a single-window approach.
WBJEEB has been instrumental in the admission process based on online application and allotment through e-Counselling since 2012. It advocates fairness and transparency, ensures no-error, and adopts state-of-the-art technology.
S.No. | Topics |
1 |
|
2 | Trigonometry |
3 | Coordinate geometry of two dimensions |
4 | Coordinate geometry of three dimensions |
5 |
|
The West Bengal Joint Entrance Examinations Board
The West Bengal Joint Entrance Examinations Board (WBJEEB) was established in 1962 by Government of West Bengal in exercise of the powers conferred under article 162 of the Constitution of India in pursuant to No. 828-Edn(T), dated 02.03.1962.
Subsequently in 2014, the Government of West Bengal enacted the West Bengal Act XIV of 2014 to form The West Bengal Joint Entrance Examinations Board and empowered it to conduct Common Entrance Examinations for selection of candidates for admission to undergraduate and postgraduate Professional, Vocational and General Degree Courses in the State of West Bengal and to conduct on-line counselling process or otherwise adopting a single-window approach.
WBJEEB has been instrumental in the admission process based on online application and allotment through e-Counselling since 2012. It advocates fairness and transparency, ensures no-error, and adopts state-of-the-art technology.
S.No. | Topics |
1 |
|
2 | Trigonometry |
3 | Coordinate geometry of two dimensions |
4 | Coordinate geometry of three dimensions |
5 |
|
A combination is a mathematical technique that determines the number of possible arrangements in a collection of items where the order of the selection does not matter. In combinations, you can select the items in any order.
Combinations can be confused with permutations. However, in permutations, the order of the selected items is essential. For example, the arrangements ab and ba are equal in combinations (considered as one arrangement), while in permutations, the arrangements are different.
Mathematically, the formula for determining the number of possible arrangements by selecting only a few objects from a set with no repetition is expressed in the following way:
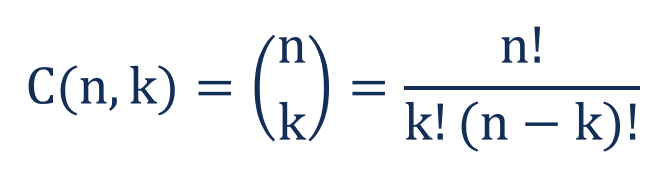
Where:
A few important results on combinations are as follows:
