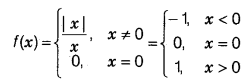Cartesian Product of Sets
Suppose there are two non-empty sets A and B. So, the cartesian product of A and B is the set of all ordered pairs of elements from A and B.
A × B = {(a,b) : a ∊ A, b ∊ B}
Let A = {a1, a2, a3, a4} and B = {b1, b2}
Then, The cartesian product of A and B will be;
A × B = {(a1, b1), (a2, b1), (a3, b1), (a4, b1), (a1, b2), (a2, b2), (a3, b2), (a4, b2)}
Example: Let us say, X = {a,b,c} and Y = { 1,2,3}
Therefore, X × Y = {(a, 1), (a, 2), (a, 3), (b, 1), (b, 2), (b, 3), (c, 1), (c, 2), (c, 3)}.
This set has 9 ordered pairs. We can also represent it as in a tabular form.
Note: Two ordered pair X and Y are equal, if and only if the corresponding first elements and second elements are equal.
Relations
Definition: A relation R is the subset of the cartesian product of X x Y, where X and Y are two non-empty elements. It is derived by stating the relationship between the first element and second element of the ordered pair of X × Y. The set of all primary elements of the ordered pairs is called a domain of R and the set of all second elements of the ordered pairs is called a range of R.
For two sets X = {a, b, c} and Y = {apple, ball, cat}, the cartesian product have 9 ordered pairs, which can be written as;
X × Y = {(a, apple), (a, ball), (a, cat), (b, apple), (b, ball), (b, cat), (c, apple), (c, ball), (c, cat)}
With this we can obtain a subset of X x Y by introducing a relation R, between the elements of X and Y as;
R = {(a,b) : a is the first letter of word b, a ∊ X, b ∊ Y}
Therefore, the relation between X and Y can be represented as;
R = {(a,apple),(b,ball),(c,cat)}
Example: Let X={a,b} and Y = {c,d}. Find the number of relations from X to Y.
Solution: X × Y = {(a,c),(a,d),(b,c),(b,d)}
Number of subsets, n (X × Y) = 24 . Therefore, the number of relations from X to Y is 24.
Solved Problems from the book of RD Sharma - Class XI CBSE