ICSE Class IX - Practice Set

Practice Set 32 Marks - Real Numbers and Compound Interest - Click Here

Practice Set 25 Marks -7 Questions- Real Numbers, Exponents, Compound Interest and Expansions - Set I

Practice Set 28 Marks-8 Questions- Real Numbers, Exponents, Compound Interest and Expansions - Set II

Practice Set 15 Questions - Real Numbers - Click Here

Harder Problems 22 Questions - Algebraic Identities - Click Here

Practice Set 39 Questions - Factorisations - Click Here

Practice Set 23 Questions - Expansion and Indices - Click Here

Practice Set 23 Questions - Real Numbers and Compound Interest - Click Here

HS MATHEMATICS PAPER English Version 2022 - XII-Question Paper and Solution - WBCHSE

 Download the full question paper and solution of mathematics for the year 2022 under WBCHSE ( West Bengal Council of Higher Secondary Education ) HS.

HS 2022 Mathematics English Version

WBJEE MATHEMATICS PAPER 2021 SOLVED

 The West Bengal Joint Entrance Examinations Board

The West Bengal Joint Entrance Examinations Board (WBJEEB) was established in 1962 by Government of West Bengal in exercise of the powers conferred under article 162 of the Constitution of India in pursuant to No. 828-Edn(T), dated 02.03.1962.

Subsequently in 2014, the Government of West Bengal enacted the West Bengal Act XIV of 2014 to form The West Bengal Joint Entrance Examinations Board and empowered it to conduct Common Entrance Examinations for selection of candidates for admission to undergraduate and postgraduate Professional, Vocational and General Degree Courses in the State of West Bengal and to conduct on-line counselling process or otherwise adopting a single-window approach.

WBJEEB has been instrumental in the admission process based on online application and allotment through e-Counselling since 2012. It advocates fairness and transparency, ensures no-error, and adopts state-of-the-art technology.

WBJEE 2022 Mathematics Syllabus

S.No.	Topics
1	Algebra Arithmetic Progression G.P., H.P Sets, Relations and Mappings Logarithms Complex Numbers Permutation and combination Polynomial equation Principle of mathematical induction Matrices Binomial theorem (positive integral index) Statistics and Probability
2	Trigonometry
3	Coordinate geometry of two dimensions
4	Coordinate geometry of three dimensions
5	Differential calculus Calculus Integral calculus Application of Calculus Differential Equations Vectors

WBJEE MATHEMATICS PAPER 2020 SOLVED

 The West Bengal Joint Entrance Examinations Board

The West Bengal Joint Entrance Examinations Board (WBJEEB) was established in 1962 by Government of West Bengal in exercise of the powers conferred under article 162 of the Constitution of India in pursuant to No. 828-Edn(T), dated 02.03.1962.

Subsequently in 2014, the Government of West Bengal enacted the West Bengal Act XIV of 2014 to form The West Bengal Joint Entrance Examinations Board and empowered it to conduct Common Entrance Examinations for selection of candidates for admission to undergraduate and postgraduate Professional, Vocational and General Degree Courses in the State of West Bengal and to conduct on-line counselling process or otherwise adopting a single-window approach.

WBJEEB has been instrumental in the admission process based on online application and allotment through e-Counselling since 2012. It advocates fairness and transparency, ensures no-error, and adopts state-of-the-art technology.

WBJEE 2022 Mathematics Syllabus

S.No.	Topics
1	Algebra Arithmetic Progression G.P., H.P Sets, Relations and Mappings Logarithms Complex Numbers Permutation and combination Polynomial equation Principle of mathematical induction Matrices Binomial theorem (positive integral index) Statistics and Probability
2	Trigonometry
3	Coordinate geometry of two dimensions
4	Coordinate geometry of three dimensions
5	Differential calculus Calculus Integral calculus Application of Calculus Differential Equations Vectors

Combinations - RD Sharma Solved Problems

 

What is a Combination?

A combination is a mathematical technique that determines the number of possible arrangements in a collection of items where the order of the selection does not matter. In combinations, you can select the items in any order.

Combinations can be confused with permutations. However, in permutations, the order of the selected items is essential. For example, the arrangements ab and ba are equal in combinations (considered as one arrangement), while in permutations, the arrangements are different.

Formula for Combination

Mathematically, the formula for determining the number of possible arrangements by selecting only a few objects from a set with no repetition is expressed in the following way:

 

 

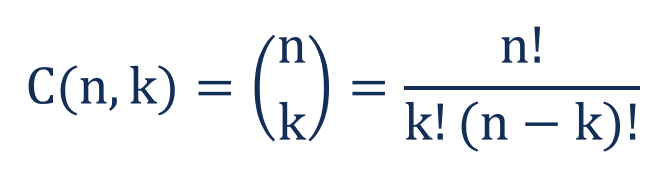
Where:

• n – the total number of elements in a set
• k – the number of selected objects (the order of the objects is not important)
• ! – factorial

A few important results on combinations are as follows:

• The number of ways of selecting n objects out of n objects is:${}^n{C}_n=\frac{n!}{n!\left(n-n\right)!}=\frac{n!}{n!0!}=1$
• The number of ways of selecting 0 objects out of n objects is:${}^n{C}_0=\frac{n!}{0!\left(n-0\right)!}=\frac{n!}{0!n!}=1$
• The number of ways of selecting 1 object out of n objects is: ${}^n{C}_1=\frac{n!}{1!\left(n-1\right)!}=\frac{n\times \left(n-1\right)!}{\left(n-1\right)!}=n$
• ${}^n{C}_r{=}^n{C}_{n-r}$
• ${}^n{C}_r{+}^n{C}_{r-1}{=}^{n+1}{C}_r$